Giovanni Volpe, Carolina Wählby, Lei Tian, Michael Hecht, Artur Yakimovich, Kristina Monakhova, Laura Waller, Ivo F. Sbalzarini, Christopher A. Metzler, Mingyang Xie, Kevin Zhang, Isaac C.D. Lenton, Halina Rubinsztein-Dunlop, Daniel Brunner, Bijie Bai, Aydogan Ozcan, Daniel Midtvedt, Hao Wang, Nataša Sladoje, Joakim Lindblad, Jason T. Smith, Marien Ochoa, Margarida Barroso, Xavier Intes, Tong Qiu, Li-Yu Yu, Sixian You, Yongtao Liu, Maxim A. Ziatdinov, Sergei V. Kalinin, Arlo Sheridan, Uri Manor, Elias Nehme, Ofri Goldenberg, Yoav Shechtman, Henrik K. Moberg, Christoph Langhammer, Barbora Špačková, Saga Helgadottir, Benjamin Midtvedt, Aykut Argun, Tobias Thalheim, Frank Cichos, Stefano Bo, Lars Hubatsch, Jesus Pineda, Carlo Manzo, Harshith Bachimanchi, Erik Selander, Antoni Homs-Corbera, Martin Fränzl, Kevin de Haan, Yair Rivenson, Zofia Korczak, Caroline Beck Adiels, Mite Mijalkov, Dániel Veréb, Yu-Wei Chang, Joana B. Pereira, Damian Matuszewski, Gustaf Kylberg, Ida-Maria Sintorn, Juan C. Caicedo, Beth A Cimini, Muyinatu A. Lediju Bell, Bruno M. Saraiva, Guillaume Jacquemet, Ricardo Henriques, Wei Ouyang, Trang Le, Estibaliz Gómez-de-Mariscal, Daniel Sage, Arrate Muñoz-Barrutia, Ebba Josefson Lindqvist, Johanna Bergman
arXiv: 2303.03793
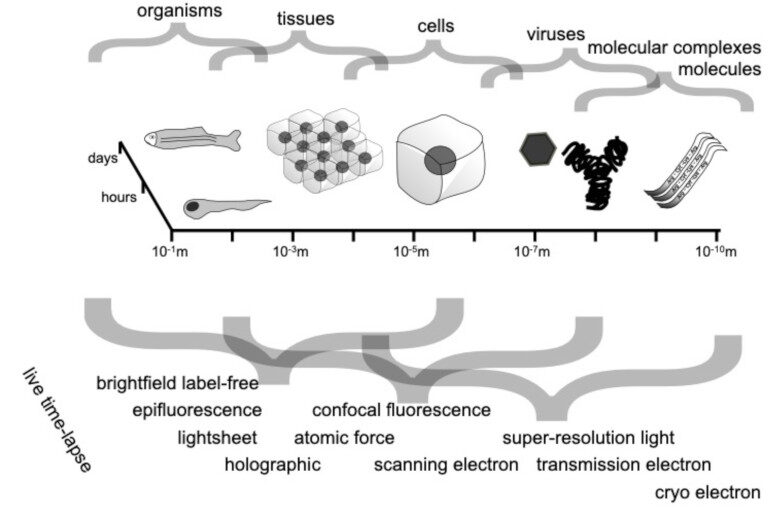
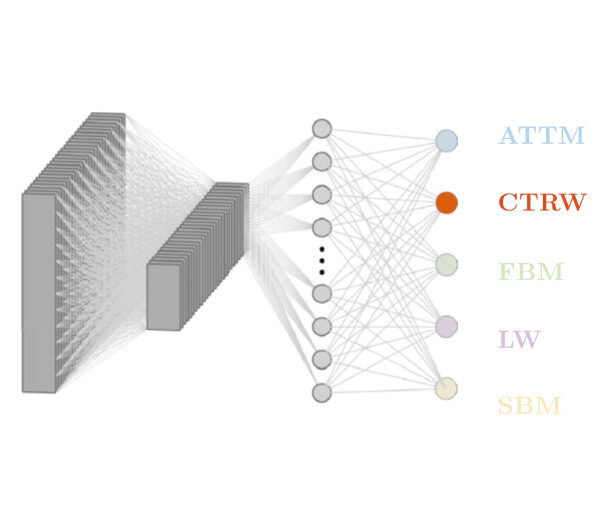
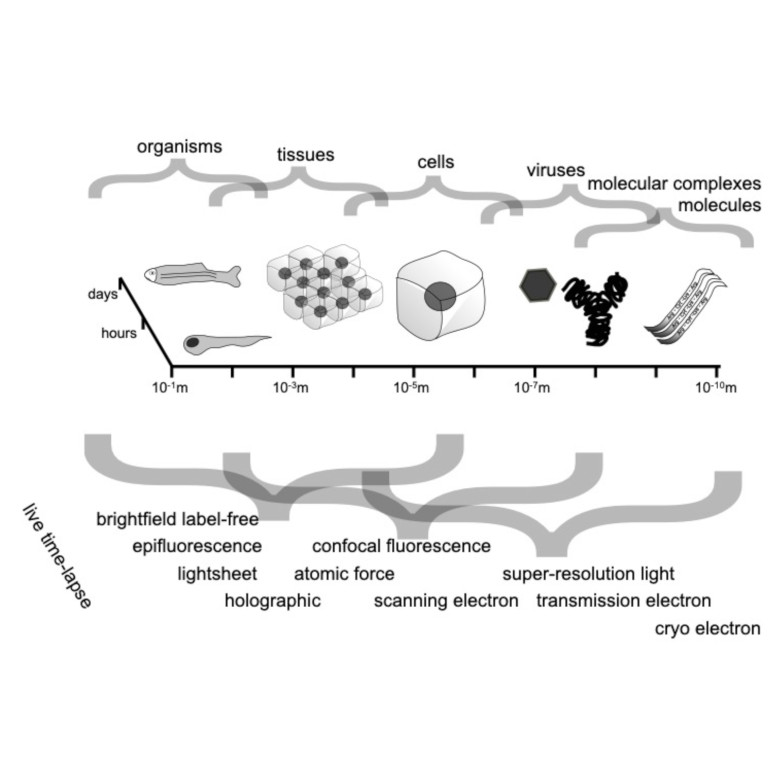
Through digital imaging, microscopy has evolved from primarily being a means for visual observation of life at the micro- and nano-scale, to a quantitative tool with ever-increasing resolution and throughput. Artificial intelligence, deep neural networks, and machine learning are all niche terms describing computational methods that have gained a pivotal role in microscopy-based research over the past decade. This Roadmap is written collectively by prominent researchers and encompasses selected aspects of how machine learning is applied to microscopy image data, with the aim of gaining scientific knowledge by improved image quality, automated detection, segmentation, classification and tracking of objects, and efficient merging of information from multiple imaging modalities. We aim to give the reader an overview of the key developments and an understanding of possibilities and limitations of machine learning for microscopy. It will be of interest to a wide cross-disciplinary audience in the physical sciences and life sciences.