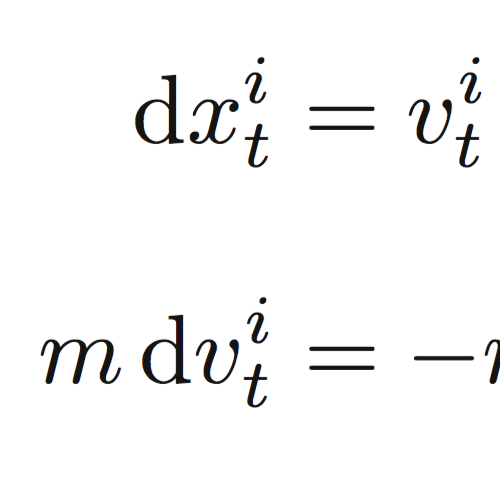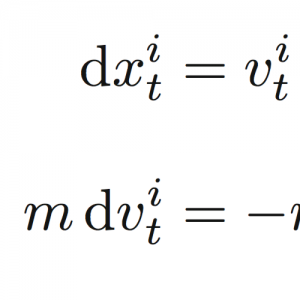
Experimental realization of a minimal microscopic heat engine
Aykut Argun, Jalpa Soni, Lennart Dabelow, Stefano Bo, Giuseppe Pesce, Ralf Eichhorn & Giovanni Volpe
Physical Review E 96(5), 052106 (2017)
DOI: 10.1103/PhysRevE.96.052106
arXiv: 1708.07197
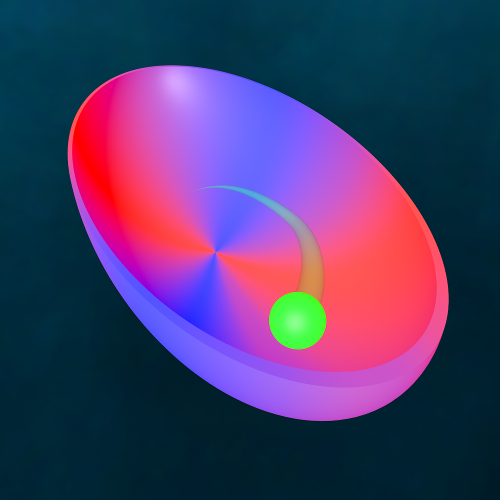
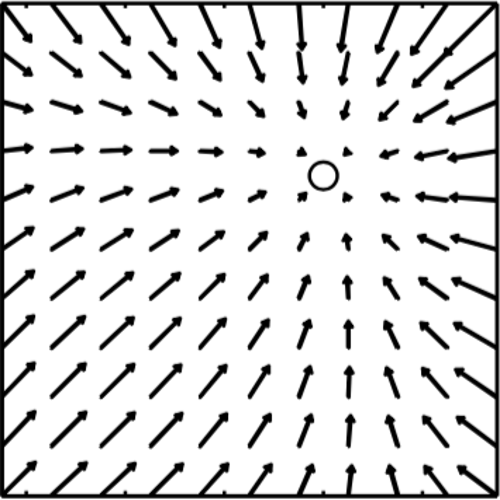
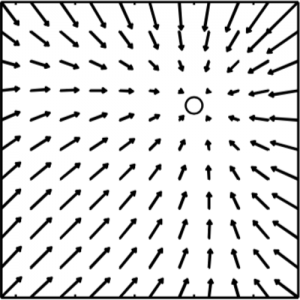
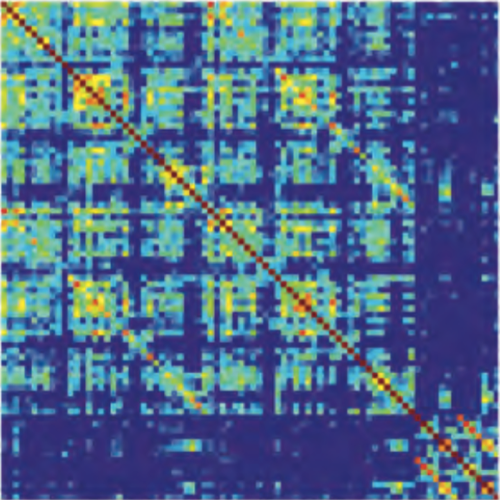
Microscopic heat engines are microscale systems that convert energy flows between heat reservoirs into work or systematic motion. We have experimentally realized a minimal microscopic heat engine. It consists of a colloidal Brownian particle optically trapped in an elliptical potential well and simultaneously coupled to two heat baths at different temperatures acting along perpendicular directions. For a generic arrangement of the principal directions of the baths and the potential, the symmetry of the system is broken, such that the heat flow drives a systematic gyrating motion of the particle around the potential minimum. Using the experimentally measured trajectories, we quantify the gyrating motion of the particle, the resulting torque that it exerts on the potential, and the associated heat flow between the heat baths. We find excellent agreement between the experimental results and the theoretical predictions.