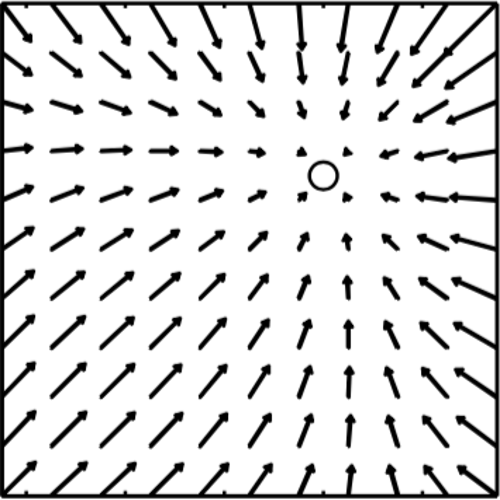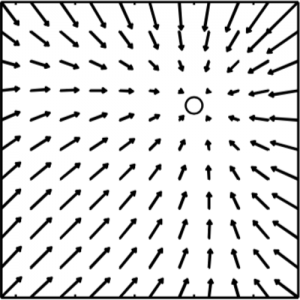
An SDE approximation for stochastic differential delay equations with colored state-dependent noise
Austin McDaniel, Ozer Duman, Giovanni Volpe & Jan Wehr
Markov Processes and Related Fields 22(3), 595-628 (2016)
arXiv: 1406.7287
We consider a general multidimensional stochastic differential delay equation (SDDE) with colored state-dependent noises. We approxi-mate it by a stochastic differential equation (SDE) system and calcu- late its limit as the time delays and the correlation times of the noises go to zero. The main result is proven using a theorem of convergence of stochastic integrals developed by Kurtz and Protter. The result formalizes and extends a method that has been used in the analysis of a noisy electrical circuit with delayed state-dependent noise, and may be further used as a working SDE approximation of an SDDE system modeling a real system, where noises are correlated in time and whose response to stimuli is delayed.