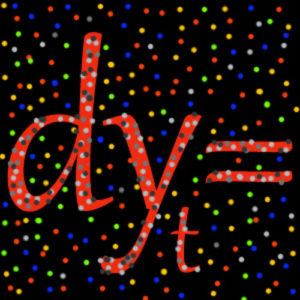
Stratonovich-to-Itô transition in noisy systems with multiplicative feedback
Giuseppe Pesce, Austin McDaniel, Scott Hottovy, Jan Wehr & Giovanni Volpe
Nature Communications 4, 2733 (2013)
DOI: 10.1038/ncomms3733
arXiv: 1206.6271
Intrinsically noisy mechanisms drive most physical, biological and economic phenomena. Frequently, the system’s state influences the driving noise intensity (multiplicative feedback). These phenomena are often modelled using stochastic differential equations, which can be interpreted according to various conventions (for example, Itô calculus and Stratonovich calculus), leading to qualitatively different solutions. Thus, a stochastic differential equation–convention pair must be determined from the available experimental data before being able to predict the system’s behaviour under new conditions. Here we experimentally demonstrate that the convention for a given system may vary with the operational conditions: we show that a noisy electric circuit shifts from obeying Stratonovich calculus to obeying Itô calculus. We track such a transition to the underlying dynamics of the system and, in particular, to the ratio between the driving noise correlation time and the feedback delay time. We discuss possible implications of our conclusions, supported by numerics, for biology and economics.
