Effective drifts in dynamical systems with multiplicative noise: A review of recent progress (Invited review)
Giovanni Volpe & Jan Wehr
Reports on Progress in Physics 79(5), 053901 (2016)
DOI: 10.1088/0034-4885/79/5/053901
arXiv: 1511.05340
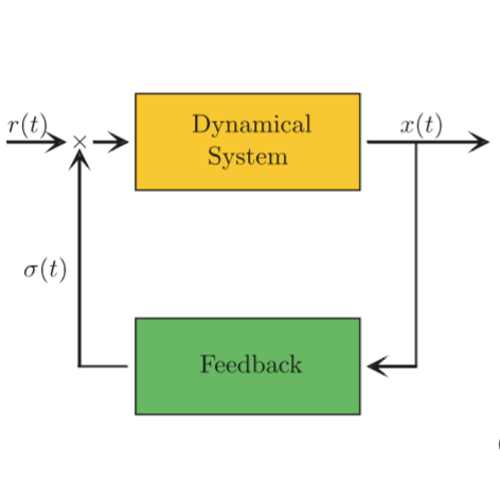
Noisy dynamical models are employed to describe a wide range of phenomena. Since exact modeling of these phenomena requires access to their microscopic dynamics, whose time scales are typically much shorter than the observable time scales, there is often need to resort to effective mathematical models such as stochastic differential equations (SDEs). In particular, here we consider effective SDEs describing the behavior of systems in the limits when natural time scales become very small. In the presence of multiplicative noise (i.e. noise whose intensity depends upon the system’s state), an additional drift term, called noise-induced drift or effective drift, appears. The nature of this noise-induced drift has been recently the subject of a growing number of theoretical and experimental
studies. Here, we provide an extensive review of the state of the art in this eld. After an introduction, we discuss a minimal model of how multiplicative noise affects the evolution of a system. Next, we consider several case studies with a focus on recent experiments: the Brownian motion of a microscopic particle in thermal equilibrium with a heat bath in the presence of a diffusion gradient; the limiting behavior of a system driven by a colored noise modulated by a multiplicative feedback; and the behavior of an autonomous agent subject to sensorial delay in a noisy environment. This allows us to present the experimental results, as well as mathematical methods and numerical techniques, that can be employed to study a wide range of systems. At the end we give an application-oriented overview of future projects involving noise-induced drifts, including both theory and experiment.