Alberto Imparato – Soft Matter Lab

Destructive effect of fluctuations on the performance of a Brownian gyrator on ArXiv

Angular velocity in the steady-state. *(Excerpt from Fig. 2 of the manuscript.)*

Destructive effect of fluctuations on the performance of a Brownian gyrator
Pascal Viot, Aykut Argun, Giovanni Volpe, Alberto Imparato, Lamberto Rondoni, Gleb Oshanin
arxiv: 2307.05248

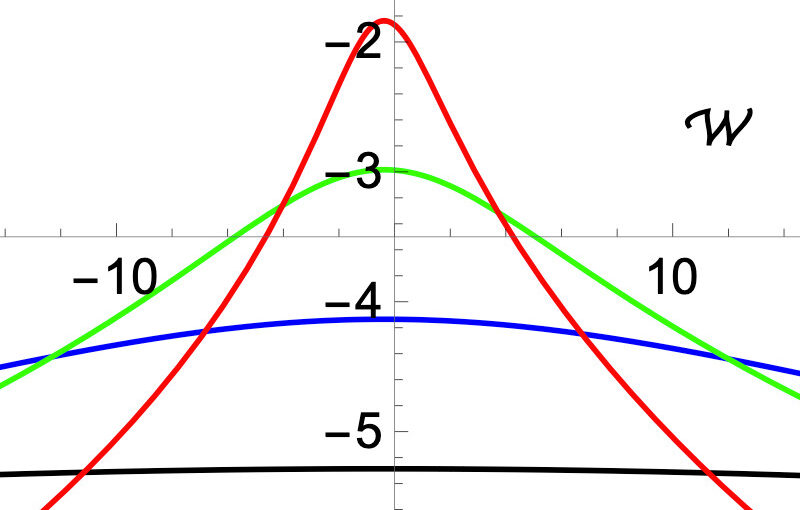
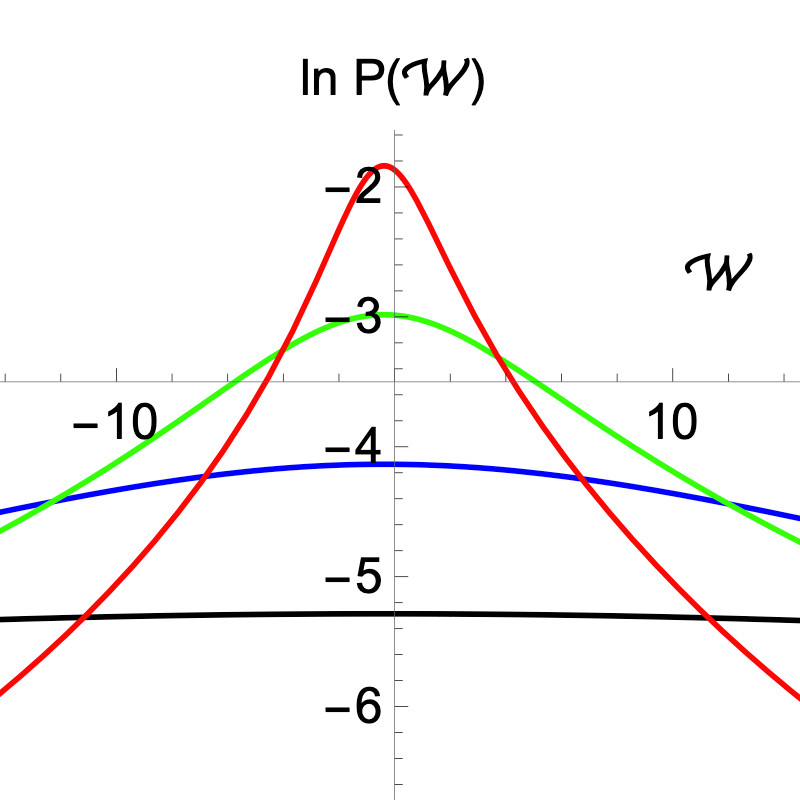
The Brownian gyrator (BG) is a minimal model of a nano-engine performing a rotational motion, judging solely upon the fact that in non-equilibrium conditions its torque, angular momentum L and angular velocity W have non-zero mean values. For a time-discretized model, we calculate the previously unknown probability density functions (PDFs) of L and W. We find that when the time-step δt → 0, both PDFs converge to uniform distributions with diverging variances. For finite δt, the PDF of L has exponential tails and all moments, but its noise-to-signal ratio is generically much bigger than 1. The PDF of W exhibits heavy power-law tails and its mean W is the only existing moment. The BG is therefore not an engine in common sense: it does not exhibit regular rotations on each run and its fluctuations are not only a minor nuisance.
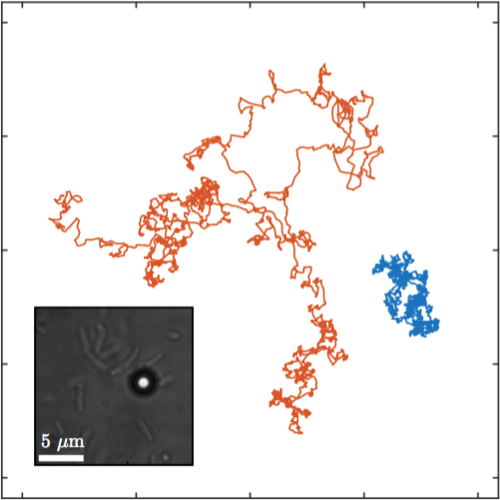
Our theoretical predictions are confirmed by numerical simulations and experimental data. We discuss some improvements of the model which may result in a more systematic behavior.

Non-Boltzmann Distributions and Non-Equilibrium Relations in Active Baths published in Phys. Rev. E

Non-Boltzmann stationary distributions and non-equilibrium relations in active baths
Aykut Argun, Ali-Reza Moradi, Erçağ Pinçe, Gokhan Baris Bagci, Alberto Imparato & Giovanni Volpe
Physical Review E 94(6), 062150 (2016)
DOI: 10.1103/PhysRevE.94.062150

Most natural and engineered processes, such as biomolecular reactions, protein folding, and population dynamics, occur far from equilibrium and therefore cannot be treated within the framework of classical equilibrium thermodynamics. Here we experimentally study how some fundamental thermodynamic quantities and relations are affected by the presence of the nonequilibrium fluctuations associated with an active bath. We show in particular that, as the confinement of the particle increases, the stationary probability distribution of a Brownian particle confined within a harmonic potential becomes non-Boltzmann, featuring a transition from a Gaussian distribution to a heavy-tailed distribution. Because of this, nonequilibrium relations (e.g., the Jarzynski equality and Crooks fluctuation theorem) cannot be applied. We show that these relations can be restored by using the effective potential associated with the stationary probability distribution. We corroborate our experimental findings with theoretical arguments.

Work Done by Rotational Force Fields published in J. Opt.

Influence of rotational force fields on the determination of the work done on a driven Brownian particle
Giuseppe Pesce, Giovanni Volpe, Alberto Imparato, Giulia Rusciano & Antonio Sasso
Journal of Optics 13(4), 044006 (2011)
DOI: 10.1088/2040-8978/13/4/044006
arXiv: 1006.4534

For a Brownian system the evolution of thermodynamic quantities is a stochastic process, in particular the work performed on a driven colloidal particle held in an optical trap, changes for each realization of the experimental manipulation, even though the manipulation protocol remains unchanged. Nevertheless, the work distribution is governed by established laws. Here, we show how the measurement of the work distribution is influenced by the presence of rotational, i.e. nonconservative, radiation forces. Experiments on particles of different materials show that the rotational radiation forces, and therefore their effect on the work distributions, increase with the particle’s refractive index.