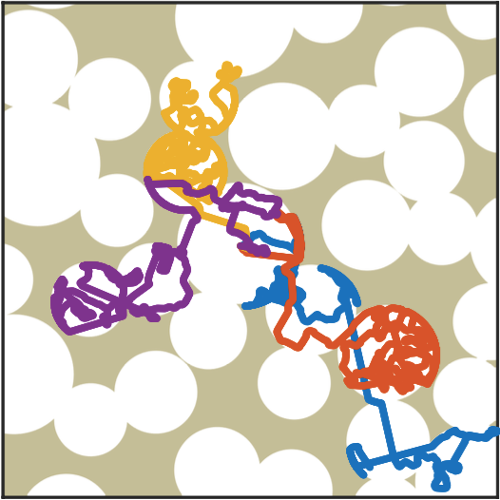
The topography of the environment alters the optimal search strategy for active particles
Giorgio Volpe & Giovanni Volpe
Proceedings of the National Academy of Science USA 114(43), 11350—11355 (2017)
DOI: 10.1073/pnas.1711371114
arXiv: 1706.07785
In environments with scarce resources, adopting the right search strategy can make the difference between succeeding and failing, even between life and death. At different scales, this applies to molecular encounters in the cell cytoplasm, to animals looking for food or mates in natural landscapes, to rescuers during search-and- rescue operations in disaster zones, and to genetic computer algo- rithms exploring parameter spaces. When looking for sparse targets in a homogeneous environment, a combination of ballistic and diffusive steps is considered optimal; in particular, more ballistic Lévy flights with exponent α ≤ 1 are generally believed to optimize the search process. However, most search spaces present complex to- pographies. What is the best search strategy in these more realistic scenarios? Here we show that the topography of the environment significantly alters the optimal search strategy towards less ballistic and more Brownian strategies. We consider an active particle performing a blind cruise search for non-regenerating sparse targets in a two-dimensional space with steps drawn from a Lévy distribution with exponent varying from α = 1 to α = 2 (Brownian). We demon- strate that, when boundaries, barriers and obstacles are present, the optimal search strategy depends on the topography of the environ- ment with α assuming intermediate values in the whole range under consideration. We interpret these findings using simple scaling arguments and discuss their robustness to varying searcher’s size. Our results are relevant for search problems at different length scales, from animal and human foraging, to microswimmers’ taxis, to bio- chemical rates of reaction.