Jan Wehr – Page 2 – Soft Matter Lab

Noise-induced drift in SDEs published in J. Stat. Phys.

Noise-induced drift in stochastic differential equations with arbitrary friction and diffusion in the Smoluchowski-Kramers limit
Scott Hottovy, Giovanni Volpe & Jan Wehr
Journal of Statistical Physics 146(4), 762—773 (2012)
DOI: 10.1007/s10955-012-0418-9
arXiv: 1112.2607

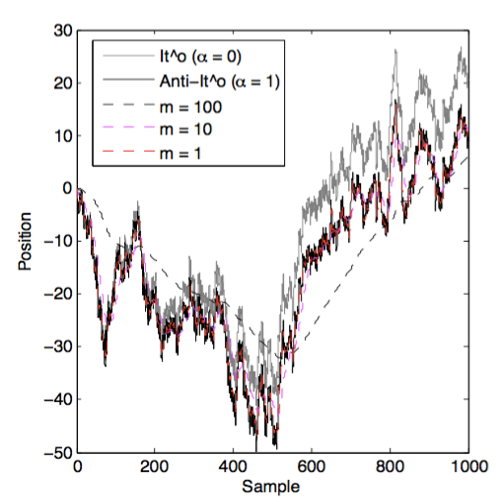
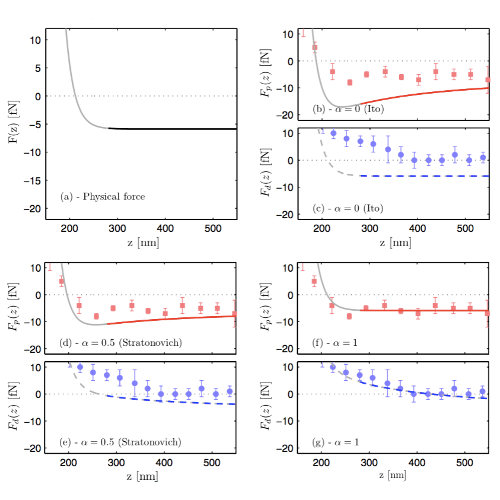
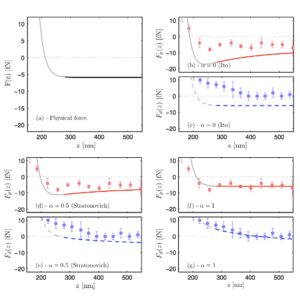
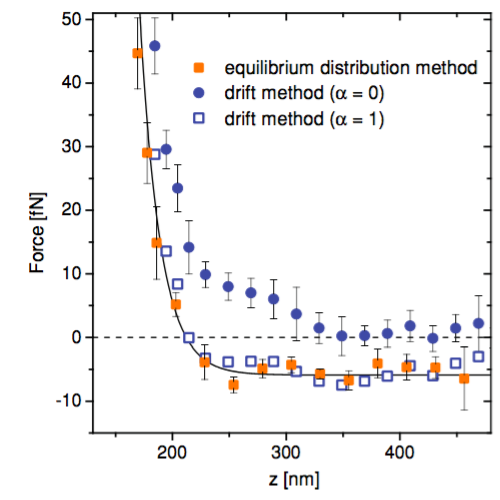
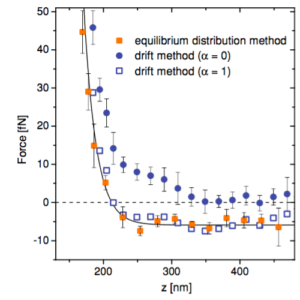
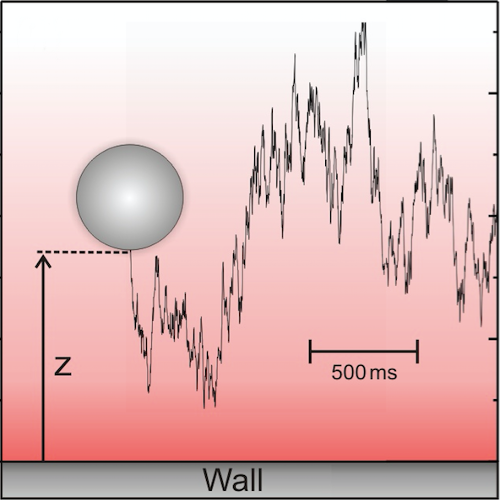
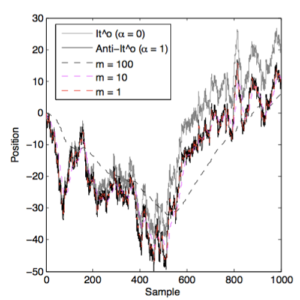
We consider the dynamics of systems with arbitrary friction and diffusion. These include, as a special case, systems for which friction and diffusion are connected by Einstein fluctuation-dissipation relation, e.g. Brownian motion. We study the limit where friction effects dominate the inertia, i.e. where the mass goes to zero (Smoluchowski-Kramers limit). Using the Itô stochastic integral convention, we show that the limiting effective Langevin equations has different drift fields depending on the relation between friction and diffusion. Alternatively, our results can be cast as different interpretations of stochastic integration in the limiting equation, which can be parametrized by α∈ℝ. Interestingly, in addition to the classical Itô (α=0), Stratonovich (α=0.5) and anti-Itô (α=1) integrals, we show that position-dependent α=α(x), and even stochastic integrals with α∉[0,1] arise. Our findings are supported by numerical simulations.

Reply to Comment on Influence of Noise on Force Measurements published in Phys. Rev. Lett.

Reply to comment on “Influence of noise on force measurements”
Giovanni Volpe, Laurent Helden, Thomas Brettschneider, Jan Wehr & Clemens Bechinger
Physical Review Letters 107(7), 078902 (2011)
DOI: 10.1103/PhysRevLett.107.078902
arXiv: 1101.3916

Comparison Between Force Measurement Methods published in Phys. Rev. E

Force measurement in the presence of Brownian noise: Equilibrium distribution method vs. drift method
Thomas Brettschneider, Giovanni Volpe, Laurent Helden, Jan Wehr & Clemens Bechinger
Physical Review E 83(4), 041113 (2011)
DOI: 10.1103/PhysRevE.83.041113
arXiv: 1009.2386

The study of microsystems and the development of nanotechnologies require alternative techniques to measure piconewton and femtonewton forces at microscopic and nanoscopic scales. Among the challenges is the need to deal with the ineluctable thermal noise, which, in the typical experimental situation of a spatial diffusion gradient, causes a spurious drift. This leads to a correction term when forces are estimated from drift measurements [G. Volpe, L. Helden, T. Brettschneider, J. Wehr, and C. Bechinger, Phys. Rev. Lett. 104, 170602 (2010)]. Here we provide a systematic study of such an effect by comparing the forces acting on various Brownian particles derived from equilibrium-distribution and drift measurements. We discuss the physical origin of the correction term, its dependence on wall distance and particle radius, and its relation to the convention used to solve the respective stochastic integrals. Such a correction term becomes more significant for smaller particles and is predicted to be on the order of several piconewtons for particles the size of a biomolecule.

Influence of Noise on Force Measurements published in Phys. Rev. Lett.

Influence of noise on force measurements
Giovanni Volpe, Laurent Helden, Thomas Brettschneider, Jan Wehr & Clemens Bechinger
Physical Review Letters 104(17), 170602 (2010)
DOI: 10.1103/PhysRevLett.104.170602
arXiv: 1004.0874

We demonstrate how the ineluctable presence of thermal noise alters the measurement of forces acting on microscopic and nanoscopic objects. We quantify this effect exemplarily for a Brownian particle near a wall subjected to gravitational and electrostatic forces. Our results demonstrate that the force-measurement process is prone to artifacts if the noise is not correctly taken into account.

Cost of Thermal Noise Suppression published in J. Phys. A.

Thermal noise suppression: How much does it cost?
Giovanni Volpe, Jan Wehr, Dmitri Petrov & J. Miguel Rubi
Journal of Physics A: Mathematical and Theoretical 42(9), 095005 (2009)
DOI: 10.1088/1751-8113/42/9/095005
arXiv: 0711.0923

In order to stabilize the behavior of noisy systems, confining it around a desirable state, an effort is required to suppress the intrinsic noise. This noise suppression task entails a cost. For the important case of thermal noise in an overdamped system, we show that the minimum cost is achieved when the system control parameters are held constant: any additional deterministic or random modulation produces an increase of the cost. We discuss the implications of this phenomenon for those overdamped systems whose control parameters are intrinsically noisy, presenting a case study based on the example of a Brownian particle optically trapped in an oscillating potential.