Optical force field reconstruction using Brownian trajectories
Laura Pérez García, Jaime Donlucas Pérez, Giorgio Volpe, Alejandro V. Arzola & Giovanni Volpe
Click here to see the slides.
Twitter Link: here.
Optical tweezers have evolved into sophisticated tools for the measurement and application of nanoscopic forces; its use ranges from mechanobiology to cooling and trapping atoms.
Despite their ever-growing interest, the methods employed to measure optical forces have not changed much in the last 30 years. The key methods measure the potential function, the autocorrelation function (ACF), or the power spectral density (PSD) of an optically trapped particle’s motion. Unfortunately, all these techniques have some drawbacks: they require large amounts of data acquired for long times (potential) or at high frequency (ACF and PSD); they cannot identify non-conservative force-field components; they can only measure the properties of stable equilibrium positions, and they require setting several parameters carefully and expertly [1]. These shortcomings have limited the possibility of measuring nanoscopic forces in many potential applications, such as experiments with non-conservative force fields and out-of-equilibrium conditions.
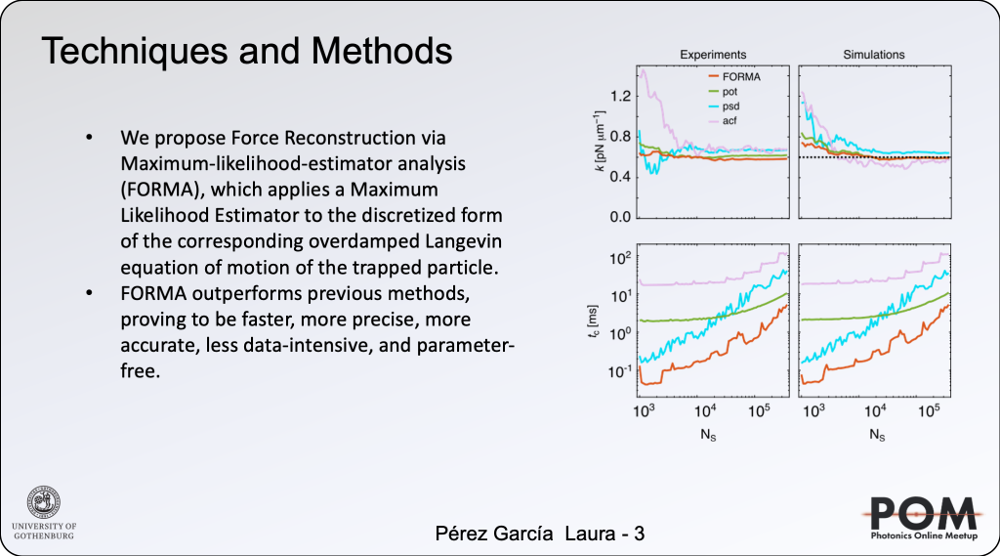
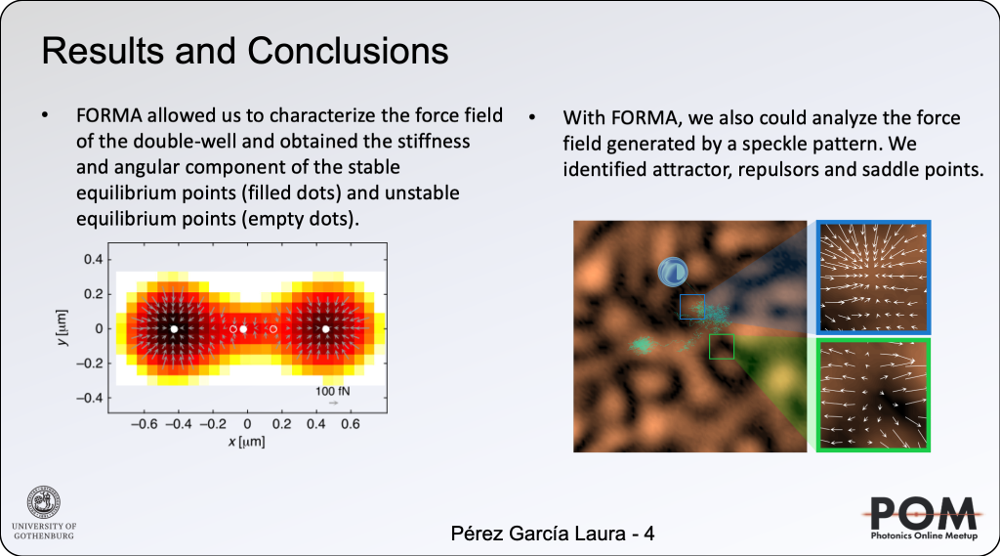
We have recently introduced a simple, robust, and fast algorithm that permits to reconstruct microscopic force fields from Brownian trajectories, Force Reconstruction via Maximum-likelihood-estimator Analysis — FORMA. FORMA exploits the fact that in the proximity of an equilibrium position, the force field can be approximated by a linear form, and therefore, optimally estimated using a linear maximum-likelihood-estimator. Its key advantages are that FORMA does not require setting analysis parameters, it executes orders-of-magnitude faster than other more standard methods, and it requires ten times fewer data to achieve the same precision and accuracy. Finally, FORMA also permits the characterization of non-conservative force fields and non-stable equilibrium positions in extended force fields [2].
References:
[1] Jones et al. Optical tweezers: Principles and applications. Cambridge, 2015.
[2] L. Pérez García, et al. Nat. Commun. 9, 5166 (2018).
Poster Session
Time: June 22nd 2020
Place: Twitter
POM Conference
Link: POM
Time: June 25th 2020
Place: Online