Soft Matter Lab

Multi-cohort and longitudinal Bayesian clustering study of stage and subtype in Alzheimer’s disease published in Nature Communications

Comparison of cluster-specific covariance matrixes with node strength. *(Image by the Authors.)*

Multi-cohort and longitudinal Bayesian clustering study of stage and subtype in Alzheimer’s disease
Konstantinos Poulakis, Joana B. Pereira, J.-Sebastian Muehlboeck, Lars-Olof Wahlund, Örjan Smedby, Giovanni Volpe, Colin L. Masters, David Ames, Yoshiki Niimi, Takeshi Iwatsubo, Daniel Ferreira, Eric Westman, Japanese Alzheimer’s Disease Neuroimaging Initiative & Australian Imaging, Biomarkers and Lifestyle study
Nature Communications 13, 4566 (2022)
doi: 10.1038/s41467-022-32202-6

Understanding Alzheimer’s disease (AD) heterogeneity is important for understanding the underlying pathophysiological mechanisms of AD. However, AD atrophy subtypes may reflect different disease stages or biologically distinct subtypes. Here we use longitudinal magnetic resonance imaging data (891 participants with AD dementia, 305 healthy control participants) from four international cohorts, and longitudinal clustering to estimate differential atrophy trajectories from the age of clinical disease onset. Our findings (in amyloid-β positive AD patients) show five distinct longitudinal patterns of atrophy with different demographical and cognitive characteristics. Some previously reported atrophy subtypes may reflect disease stages rather than distinct subtypes. The heterogeneity in atrophy rates and cognitive decline within the five longitudinal atrophy patterns, potentially expresses a complex combination of protective/risk factors and concomitant non-AD pathologies. By alternating between the cross-sectional and longitudinal understanding of AD subtypes these analyses may allow better understanding of disease heterogeneity.

Presentation by Murat Nurati Yesibolati, 4 August 2022

Measuring translational and rotational dynamics of colloid nanoparticles at the nanoscale with liquid-phase transmission electron microscopy
Murat Nulati Yesibolati, Assistant professor, Technical University of Denmark
4 August 2022, 10:30 CEST

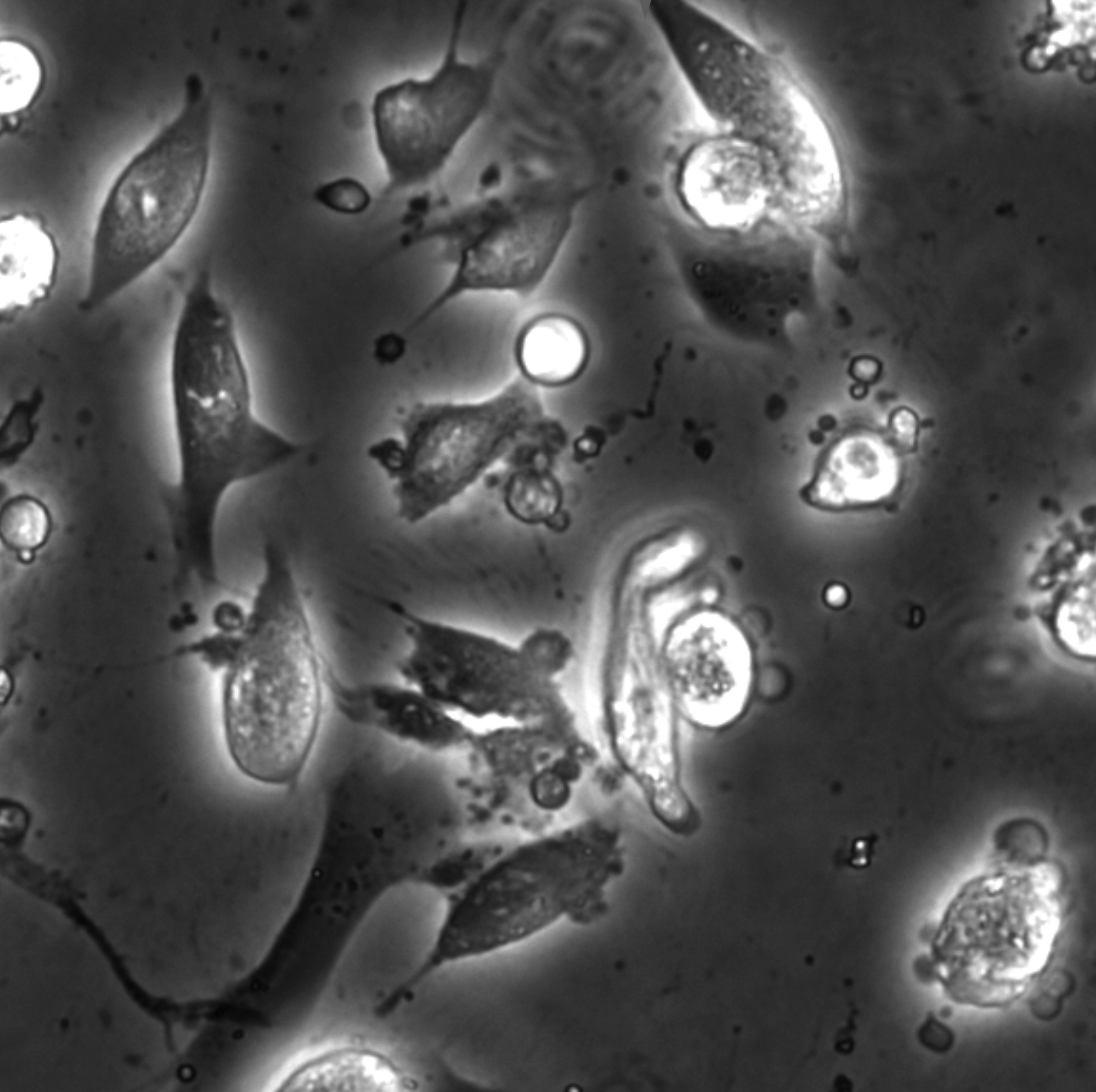
How nanoparticles (NPs) in a liquid suspension grow, transport, and interact with each other and surrounding interfaces are of fundamental interest in the colloidal matter, biomedical applications, microfluidics, and artificial micro/nanoscopic motors. Traditionally, imaging of such liquid processes has been limited to optical microscopy (OM). Bulk-level methods such as conventional OM and light scattering methods such as dynamic light scattering (DLS) cannot deliver nanometer spatial resolution at the single-particle level. Recently, liquid-phase transmission electron microscopy (LPTEM) [1] has revolutionized the access to the nanoscale, label-free imaging of a wide variety of liquid processes. Typically, the liquid cells used for LPTEM consist of electron-transparent silicon nitride (SiNx) windows suspended on two Si chips, which enclose a liquid sample layer with a thickness ranging from a few hundred nanometers to a couple of microns. With LPTEM, NP dynamics, such as nucleation and growth, self-assembly, and interactions, have been studied with sub-nanometer spatial resolution and millisecond temporal resolution.
We demonstrate how LPTEM can be used to measure the motion of individual NPs and agglomerates. Only at low electron flux do we find that individual NPs exhibit Brownian motion consistent with optical control experiments and theoretical predictions for unhindered passive diffusive motion in bulk liquids [2]. For increasing electron flux, we find increasingly faster than passive motion that still appears effectively Brownian. We discuss the possible origins of this beam–sample interaction. This establishes conditions for the use of LPTEM as a reliable tool for imaging nanoscale hydrodynamics at the nanoscale.

Bio
Murat N. Yesibolati is an Assistant Professor at Technical University of Denmark (DTU), Denmark. Murat defended his Ph.D. thesis titled “Electron holography and particle dynamics in liquid phase transmission electron microscopy” at DTU in 06.2018 under the supervision of Prof. Kristian Mølhave, DTU. Currently, he is focusing on developing a novel nanochannel liquid cell and exploring mass transport in nanochannels using advanced transmission electron microscopy. His research was supported by the Technical University of Denmark, by the Danish Research Council for Technology, grant no. 12-126194, the Advanced Materials for Energy-Water Systems (AMEWS) Center, Office of Science, Basic Energy Sciences, USA, grant number DE-AC02-06CH11357, and the VILLUM foundation, grant number 00028273.

References
[1] de Jonge, N. and F.M. Ross, Electron microscopy of specimens in liquid. Nature Nanotechnology, 2011. 6: p. 695.
[2] Yesibolati, M.N., et al., Unhindered Brownian Motion of Individual Nanoparticles in Liquid-Phase Scanning Transmission Electron Microscopy. Nano Letters, 2020. 20(10): p. 7108-7115.

Place: Nexus
Date: 4 August 2022
Time: 10:30 CEST

Invited Talk by G. Volpe at Nordita, Stockholm, 2 August 2022

Interplay between active particles and their environment
Giovanni Volpe
2 August 2022, 10:30 (CEST)
Nordita workshop: Current and Future Themes in Soft and Biological Active Matter
Albano Building 3
Stockholm, 25 July-19 August 2022

In this seminar, I will present some examples of how the behaviour of active particles can be influenced by their environment. In particular, I’ll show the formation of active molecules and active droploids from passive colloidal building blocks; the emergence of non-Boltzmann statistics and active-depletion forces between plates in an active bath; and the environment topography alters the way to multicellularity in the bacterium Myxococcus xanthus.

Marcel Rey joins the Soft Matter Lab

Marcel Rey started his post-doc at the Physics Department of the University of Gothenburg on 1st August 2022. His research is funded by a Marie-Curie Individual Fellowship with Grant No. 101064381.

Marcel received a PhD degree in Chemical-Engineering from the Friedrich-Alexander University Erlangen-Nuremberg, Germany. In his thesis, he focused on the self-assembly behavior of soft colloidal particles confined at liquid interfaces.

In the Soft Matter Lab, Marcel will investigate the “Coffee Ring Effect”, a characteristic drying behavior of liquids containing dispersed particles. The goal is to find simple strategies towards homogeneous drying of particle dispersions.

Unraveling Parkinson’s disease heterogeneity using subtypes based on multimodal data published in Parkinsonism and Related Disorders

Particular of the brain in the group comparison analysis. *(Image by the Authors.)*

Unraveling Parkinson’s disease heterogeneity using subtypes based on multimodal data
Franziska Albrecht, Konstantinos Poulakis, Malin Freidle, Hanna Johansson, Urban Ekman, Giovanni Volpe, Eric Westman, Joana B. Pereira, Erika Franzén
Parkinsonism and Related Disorders 102, 19-29 (2022)
doi: 10.1016/j.parkreldis.2022.07.014

Background

Parkinson’s disease (PD) is a clinically and neuroanatomically heterogeneous neurodegenerative disease characterized by different subtypes. To this date, no studies have used multimodal data that combines clinical, motor, cognitive and neuroimaging assessments to identify these subtypes, which may provide complementary, clinically relevant information. To address this limitation, we subtyped participants with mild-moderate PD based on a rich, multimodal dataset of clinical, cognitive, motor, and neuroimaging variables.

Methods

Cross-sectional data from 95 PD participants from our randomized EXPANd (EXercise in PArkinson’s disease and Neuroplasticity) controlled trial were included. Participants were subtyped using clinical, motor, and cognitive assessments as well as structural and resting-state MRI data. Subtyping was done by random forest clustering. We extracted information about the subtypes by inspecting their neuroimaging profiles and descriptive statistics.

Results

Our multimodal subtyping analysis yielded three PD subtypes: a motor-cognitive subtype characterized by widespread alterations in brain structure and function as well as impairment in motor and cognitive abilities; a cognitive dominant subtype mainly impaired in cognitive function that showed frontoparietal structural and functional changes; and a motor dominant subtype impaired in motor variables without any brain alterations. Motor variables were most important for the subtyping, followed by gray matter volume in the right medial postcentral gyrus.

Conclusions

Three distinct PD subtypes were identified in our multimodal dataset. The most important features to subtype PD participants were motor variables in addition to structural MRI in the sensorimotor region. These findings have the potential to improve our understanding of PD heterogeneity, which in turn can lead to personalized interventions and rehabilitation.

Invited Talk by G. Volpe at MoLE Conference 2022, Donostia/San Sebastián, Spain, 27 July 2022

Artificial intelligence in microscopy, photonics, and active matter
Giovanni Volpe
27 July 2022, 12:40 (CEST)
MoLE Conference 2022
Donostia/San Sebastián, Spain, 25-29 July 2022

After a brief overview of artificial intelligence, machine learning and deep learning, I will present a series of recent works in which we have employed deep learning for applications in microscopy, optical tweezers, and active matter. In particular, I will explain how we employed deep learning to enhance digital video microscopy, to perform virtual staining of tissues, to estimate the properties of anomalous diffusion, to characterize microscopic force fields, to improve the calculation of optical forces, and to characterize nanoparticles. Finally, I will provide an outlook on the future for the application of deep learning in these fields.

Dynamic live/apoptotic cell assay using phase-contrast imaging and deep learning on bioRxiv

Phase-contrast image before virtual staining. *(Image by the Authors.)*

Dynamic live/apoptotic cell assay using phase-contrast imaging and deep learning
Zofia Korczak, Jesús Pineda, Saga Helgadottir, Benjamin Midtvedt, Mattias Goksör, Giovanni Volpe, Caroline B. Adiels
bioRxiv: https://doi.org/10.1101/2022.07.18.500422

Chemical live/dead assay has a long history of providing information about the viability of cells cultured in vitro. The standard methods rely on imaging chemically-stained cells using fluorescence microscopy and further analysis of the obtained images to retrieve the proportion of living cells in the sample. However, such a technique is not only time-consuming but also invasive. Due to the toxicity of chemical dyes, once a sample is stained, it is discarded, meaning that longitudinal studies are impossible using this approach. Further, information about when cells start programmed cell death (apoptosis) is more relevant for dynamic studies. Here, we present an alternative method where cell images from phase-contrast time-lapse microscopy are virtually-stained using deep learning. In this study, human endothelial cells are stained live or apoptotic and subsequently counted using the self-supervised single-shot deep-learning technique (LodeSTAR). Our approach is less labour-intensive than traditional chemical staining procedures and provides dynamic live/apoptotic cell ratios from a continuous cell population with minimal impact. Further, it can be used to extract data from dense cell samples, where manual counting is unfeasible.

Neural Network Training with Highly Incomplete Datasets published in Machine Learning: Science and Technology

Working principles for training neural networks with highly incomplete dataset: vanilla (upper panel) vs GapNet (lower panel) *(Image by Yu-Wei Chang.)*

Neural Network Training with Highly Incomplete Datasets
Yu-Wei Chang, Laura Natali, Oveis Jamialahmadi, Stefano Romeo, Joana B. Pereira, Giovanni Volpe
Machine Learning: Science and Technology 3, 035001 (2022)
arXiV: 2107.00429
doi: 10.1088/2632-2153/ac7b69

Neural network training and validation rely on the availability of large high-quality datasets. However, in many cases only incomplete datasets are available, particularly in health care applications, where each patient typically undergoes different clinical procedures or can drop out of a study. Since the data to train the neural networks need to be complete, most studies discard the incomplete datapoints, which reduces the size of the training data, or impute the missing features, which can lead to artefacts. Alas, both approaches are inadequate when a large portion of the data is missing. Here, we introduce GapNet, an alternative deep-learning training approach that can use highly incomplete datasets. First, the dataset is split into subsets of samples containing all values for a certain cluster of features. Then, these subsets are used to train individual neural networks. Finally, this ensemble of neural networks is combined into a single neural network whose training is fine-tuned using all complete datapoints. Using two highly incomplete real-world medical datasets, we show that GapNet improves the identification of patients with underlying Alzheimer’s disease pathology and of patients at risk of hospitalization due to Covid-19. By distilling the information available in incomplete datasets without having to reduce their size or to impute missing values, GapNet will permit to extract valuable information from a wide range of datasets, benefiting diverse fields from medicine to engineering.

Invited Talk by G. Volpe at Active and Intelligent Living Matter Conference, Erice, 30 June 2022

Artificial intelligence in microscopy, photonics, and active matter
Giovanni Volpe
30 June 2022, 16:20 (CEST)
Active and Intelligent Living Matter Conference
Erice, Italy, 26 June-1 July 2022

Kunli Xiong joins the Soft Matter Lab

Kunli Xiong started his research position at the Physics Department of the University of Gothenburg on 16th June 2022.

Kunli received a Ph.D. degree in Material Science from the Chalmers University of Technology, Sweden. In his research, he focuses on developing novel plasmonic E-paper technology.