Non-Boltzmann stationary distributions and non-equilibrium relations in active baths
Aykut Argun, Ali-Reza Moradi, Erçağ Pinçe, Gokhan Baris Bagci, Alberto Imparato & Giovanni Volpe
Physical Review E 94(6), 062150 (2016)
DOI: 10.1103/PhysRevE.94.062150
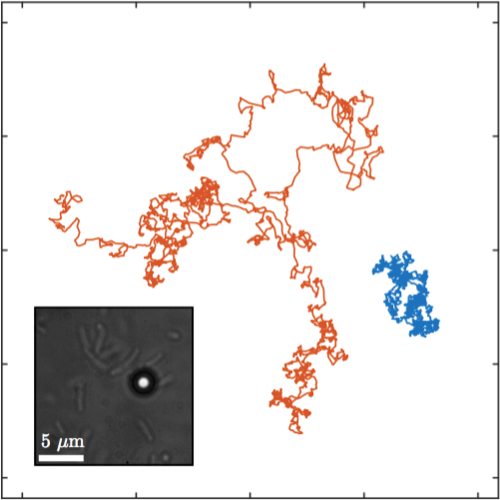
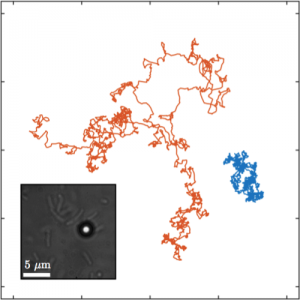
Most natural and engineered processes, such as biomolecular reactions, protein folding, and population dynamics, occur far from equilibrium and therefore cannot be treated within the framework of classical equilibrium thermodynamics. Here we experimentally study how some fundamental thermodynamic quantities and relations are affected by the presence of the nonequilibrium fluctuations associated with an active bath. We show in particular that, as the confinement of the particle increases, the stationary probability distribution of a Brownian particle confined within a harmonic potential becomes non-Boltzmann, featuring a transition from a Gaussian distribution to a heavy-tailed distribution. Because of this, nonequilibrium relations (e.g., the Jarzynski equality and Crooks fluctuation theorem) cannot be applied. We show that these relations can be restored by using the effective potential associated with the stationary probability distribution. We corroborate our experimental findings with theoretical arguments.